Data at the ratio level cannot be put in order. One cannot say that someone with an IQ of 140 is twice as intelligent as someone with an IQ of 70 because IQ is measured at the interval level but one can say that someone with six siblings has twice as many as someone with three because.

Scales Of Measurement Nominal Ordinal Interval Ratio Scale Data Youtube
False a true statement is data at a ratio level can be placed in meaningful order.
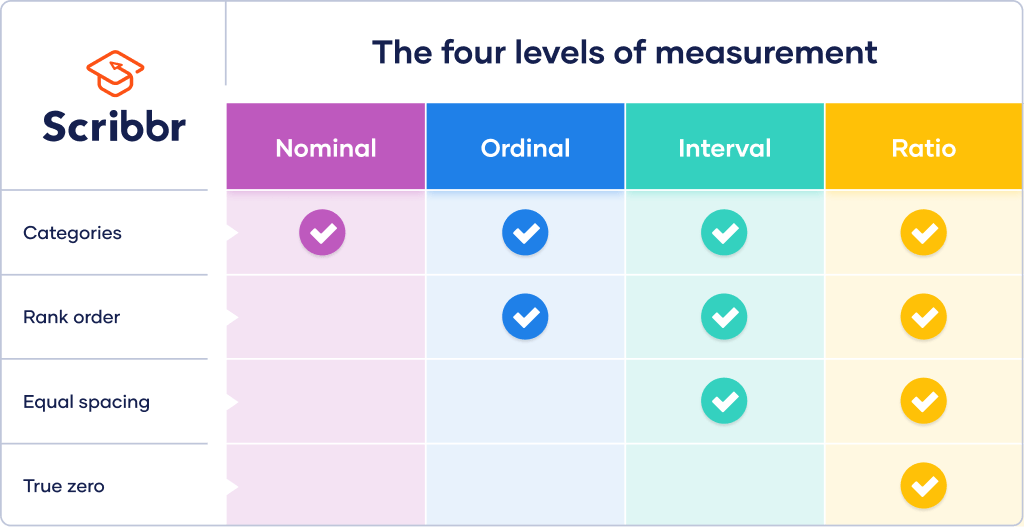
. However they cannot and do not replace the work of manual data collection and generating the actual data distribution. A true statement is Data at the ratio level can be placed in a meaningful order. There is a hierarchy in the complexity and precision of the level of measurement from low nominal to high ratio.
The data are qualitative or identify the data sets level of measurement. The last and most sophisticated level of measurement is the ratio level. This comparison is impossible in interval data.
And like the interval level we can measure the intervals between the ranks with a measurable scale of values. In ratio data the difference between 1 and 2 is the same as the difference between 3 and 4 but also here 4 is twice as much as 2. More types of calculations can be performed with data at the interval level than with data at the nominal level.
Also ratio-level measurement is the only level that allows meaningful statements about ratios of scores. Once again one cannot say that someone with an IQ of 140 is twice as intelligent as someone with an IQ of 70 because IQ is measured at the interval level but one can say that someone with six siblings has twice as many as someone with. Examples of interval level data include temperature and year.
Determine whether the following statement is true or false. False a true statement is data at the ratio level can be ordered although it. The regions with the six highest volumes of sales for a corporation last year are shown below.
Put options are used to hedge against market weakness or bet on a decline. Data at the ratio level cannot be put in order. To do this I am showing my data as a percentage ratio over day0 Day1MeanDay0Mean100.
To make it more clear. Poutcome Going by the given Dataset poutcome is a nominal attribute as it shows outcome of the previous marketing campaign. So given a distribution and a set of values we can determine the probability that the data will lie within a certain range.
Examples of ratio level data include distance and area eg acreage. According to the dataset there is only one value which is 0 which cannot be ranked or put into an order therefore it is a nominal attribute type. Also ratio-level measurement is the only level that allows meaningful statements about ratios of scores.
Ratio data can be multiplied and divided and this is one of the significant differences between ratio data and interval data which can only be added and subtracted. Unlike nominal- and ordinal-level data which are qualitative in nature interval- and ratio-level data are quantitative. If it is false rewrite it as a true statementData at the ratio level cannot be put in orderCho.
The data can be categorized ranked evenly spaced and has a natural zero. Depending on the level of measurement of the variable what you can do to analyze your data may be limited. False a true statement is data at a ratio level can be placed in meaningful order d.
Distributions show what percentage of the data lies within a certain range. One cannot say that someone with an IQ of 140 is twice as intelligent as someone with an IQ of 70 because IQ is measured at the interval level but one can say that someone with six siblings has twice as many as someone with three because. Data at the ratio level cannot be put in order.
The statement is true. Statistics and Probability questions and answers. The statement is true b.
The statement is false. True or false. Phrases such as four times and twice are meaningful at the ratio level.
But unlike the interval level we now have meaningful zero. Also ratio-level measurement is the only level that allows meaningful statements about ratios of scores. Ratio level of measurement Applies to data that can be arranged in order.
The PutCall Ratio is an indicator that shows put volume relative to call volume. My problem is that I need to show these data not as raw data but as a ratio over the first Day in order to better show the decrease in the cell number overtime. Interval and ratio are the two highest levels of measurement in Stevens original system.
Data at the ratio level cannot be put in order. False data at the ratio level can be ordered although it is impossible to determine if one data value is a multiple of another c. True or false data at the ratio level cannot be put in order a.
Due to the presence of a zero it now makes sense to compare the ratios of measurements. Also ratio-level measurement is the only level that allows meaningful statements about ratios of scores. By signing up youll get thousands of step-by-step solutions to your.
The PutCall Ratio is above 1 when put volume exceeds call volume and below 1 when call volume exceeds put volume. Negative impact of the gap between current level and steady-state level of output per capita on rate of capital accumulation recall 0 εf k 1. Data at the ratio level possess all of the features of the interval level in addition to a zero value.
Data at the ratio level cannot. In progress 0 Mathematics Eirian 5 months 2021-08-11T0606490000 2021-08-11T0606490000 1 Answers 23 views 0. The fourth and highest level of measurement is the ratio level.
Call options are used to hedge against market strength or bet on an advance. False data at the ratio level can be ordered although it is impossible to determine if one data value is a multiple of another. As with the ordinal and interval levels the data have an inherent order.
We can take the difference between data values AND find the ratio between data values ie x is twice as long as y. The lower is y t relative to y t hence the lower is k t relative to k the greater is f k k and this leads to faster growth in the eective capital-labor ratio. One cannot say that someone with an IQ of 140 is twice as intelligent as someone with an IQ of 70 because IQ is measured at the interval level but one can say that someone with six siblings has twice as many as someone with three because.

What Is Ratio Data Definition Examples Analysis
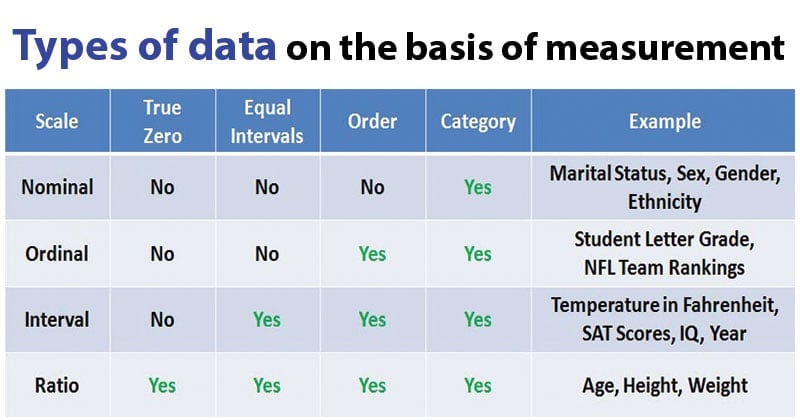
0 Comments